Représentation des données
[Mise à jour le 19/10/2023]
Sources
- Numérique et sciences informatiques 1er - ellipses
Ressources
1. Introduction
Les données et les programmes stockés dans la mémoire des machines numériques sont représentés à l'aide de deux chiffres : 0 et 1.
Ces chiffres binaires sont regroupés en paquets de 8 bits (octets ou bytes) puis couramment organisés en mots de 2, 4 ou 8 octets. Une machine dite 32 bits manipule des mots de 4 octets lorsqu'elle effectue des opérations. Ce regroupement de bits est à la base de la représentation des entiers, des réels et des caractères.
2. Encodage des entiers naturels
2.1 Écriture en base 2
Une séquence de chiffres binaires peut s'interpréter comme un nombre écrit en base 2. Dans cette base, les chiffres 0 et 1 d'une séquence sont associés à un poids 2i qui dépend de la position i des chiffres dans la séquence.
$$N_{10} = b_{n-1}2^{n-1}+b_{n-2}2^{n-2}+ ... +b_12^1+b_02^0 = \displaystyle\sum_{i=0}^{i=n-1}b_i2^i$$
ATTENTION
Cet encodage permet de représenter des entiers dans l'intervalle [0,2n - 1]
Exemples
- Un octet (n = 8) permet de coder tous les nombres entre 0 et 255
- 100110112 = 1*27 + 0*26 + 0*25 + 1*24 + 1*23 + 0*22 + 1*21 + 1*20 = 128 + 16 + 8 + 2 + 1 = 15510
2.2 Écriture en base 16
La base 16 ou hexadécimale est souvent utilisée pour simplifier l'écriture des nombres binaires.
Exemple 1001 1110 0111 01012 = 9E7516
2.3 Boutisme
Sources
- Boutisme sur Wikipédia
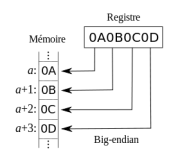 La représentation en machine des entiers naturels sur des mots de 2, 4 ou 8 octets se heurte au problème de l'ordre dans lequel ces octets sont organisés en mémoire. Ce problème est appelé le boutisme (ou endianness).
La représentation en machine des entiers naturels sur des mots de 2, 4 ou 8 octets se heurte au problème de l'ordre dans lequel ces octets sont organisés en mémoire. Ce problème est appelé le boutisme (ou endianness).
- Big endian
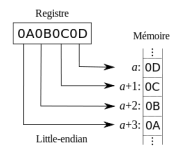
- Little endian

2.4 Bases 2,10 et 16 en Python
3. Encodage des entiers relatifs (complément à 2)
Ressource
- La notation en complément à 2 sur Wikipédia et SlidePlayer
Le code complément à 2 permet d'effectuer simplement des opérations arithmétiques sur les entiers relatifs codés en binaire. Il opère toujours sur des nombres binaires ayant le même nombre de bits (par commodité, celui-ci est généralement un multiple de 4). Wikipédia
ATTENTION
Le code complément à 2 permet de représenter des entiers dans l'intervalle [-2n-1,2n-1 - 1]. Le bit de poids fort (bit le plus à gauche) ou MSB (Most Significant Bit) donne le signe du nombre représenté (0 ⇒ positif ou 1 ⇒ négatif).
Exemple
- Un octet (n = 8) permet de coder en complément à 2 tous les nombres entre -128 et 127.
- Le nombre 011100012 est positif et égal à 8910
- Le nombre 111111112 est négatif et égal à -110
Obtention d'un nombre binaire en complément à 2
Exemple : nombre de bits nécessaires pour coder -12500010
-2n-1 ≤ -125000
⇒ 2n-1 > 125000
⇒ log10(2n-1) > log10(125000) or log10(ab) = b*log10(a)
⇒ n-1 > log10(125000)/log10(2)
⇒ n > (log10(125000)/log10(2)) + 1
⇒ n > 17,93 ⇒ n=18
Vérification : pour n = 18, N10 ∈ [-217, 217-1] soit -131072 ≤ N10 ≤ 131071
- Les nombres positifs sont représentés de manière usuelle.
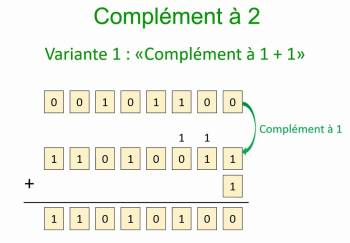
- Les nombres négatifs sont obtenus en calculant l'opposé du nombre positif par deux opérations successives:
- On inverse les bits de l'écriture binaire (opération binaire NON), on fait ce qu'on appelle le complément à un ;
- On ajoute 1 au résultat (les dépassements sont ignorés).
Cette opération correspond au calcul de 2n − |x|, où n est la longueur de la représentation et |x| la valeur absolue du nombre à coder.
Ainsi, −1 s'écrit comme 256−1 = 255 = 111111112, pour les nombres sur 8 bits. Ceci est à l'origine du nom de cette opération : « complément à 2 puissance n », quasi-systématiquement tronqué en « complément à 2 ».
La même opération effectuée sur un nombre négatif donne le nombre positif de départ: 2n − (2n − x) = x.
4. Représentation approximative des nombres réels
4.1 Nombres décimaux
L'encodage des nombres flottants est inspiré de l'écriture scientifique des nombres décimaux qui se compose d'un signe (+ ou -), d'un nombre décimal m appelé mantisse, compris dans l'intervalle [1, 10[ et d'un entier relatif n appelé exposant. L'écriture scientifique d'un nombre décimal est de la forme ±m x 10n.
4.2 Norme IEEE 754
Ressource
- IEEE 754 Wikipédia
Présentation
La représentation des nombres flottants et les opérations arithmétiques sur ces nombres a été définit par la norme IEEE 754. C'est la norme couramment utilisée dans les ordinateurs. Selon la précision souhaitée, la norme définit un format sur 32 bits (simple précision) et un autre sur 64 bits (double précision).
s : signe (0 ⇒ positif, 1 ⇒ négatif)
m : mantisse comprise dans l'intervalle [1,2[
e : exposant, décalé (biaisé) d'une valeur d qui dépend du format choisi (32 ou 64bits)
Remarques
- La mantisse est comprise dans l'intervalle [1,2[ donc m est toujours de la forme 1,xxxx. Aussi pour gagner 1 bit, on ne stocke que les chiffres après la virgule, qu'on appelle la fraction.
- L'exposant peut être positif ou négatif. Cependant, la représentation habituelle des nombres signés (complément à 2) n'est pas utilisée car, elle rendrait la comparaison entre les nombres flottants un peu plus difficile. Pour régler ce problème, l'exposant est « biaisé », afin de le stocker sous forme d'un nombre non signé.
Format simple précision (32 bits)
Un nombre flottant simple précision est stocké dans un mot de 32 bits : 1 bit de signe, 8 bits pour l'exposant et 23 bits pour la mantisse.
Pour le format 32 bits, l'exposant décalé (e-d) est un entier sur 8bits qui représente les nombres entre 0 et 255. d=127, on représente ainsi des exposants signés dans l'intervalle [-126, 127] car, 0 et 255 représentent des nombres particuliers (voir tableau des valeurs spéciales).
Exemple
Conversion en décimal de N2 = 1 10001100 1010110110000000000000
- signe = -11 = -1
- exposant = (27 + 23 + 22) - 127 = (128 + 4 + 2) - 127 = 7
- mantisse = 1 + 2-1 + 2-3 + 2-5 + 2-6 + 2 + 2-8 + 2-9 = 1,677734375
donc N10 = - 1,677734375 * 27 = -214,75
Tableau récapitulatif simple précision, double précision
| exposant (e) | fraction (f) | valeur | |
|---|---|---|---|
| 32 bits | 8 bits | 32 bits | (-1)s x 1,f x 2(e-127)) |
| 64 bits | 11 bits | 52 bits | (-1)s x 1,f x 2(e-1023)) |
s : signe (0 ⇒ positif, 1 ⇒ négatif)
f : fraction de la mantisse m
e : exposant
Valeurs spéciales
Le format des nombres flottant ne permettant pas de représenter le nombre 0, la norme IEE 754 utilise les valeurs de l'exposant 0 et 255 pour remédier à ce problème et représenter d'autres valeurs spéciales.
| Signe | Exposant | Fraction | Valeur spéciale |
|---|---|---|---|
| 0 | 0 | 0 | +0 |
| 1 | 0 | 0 | -0 |
| 0 | 255 | 0 | +∞ |
| 1 | 255 | 0 | -∞ |
| 0 | 255 | ≠0 | NaN |
NaN : Not a Number permet de représenter des résultats d'opérations invalides (0/0 etc.)
Nombres dénormalisés
Dans la représentation précédente (normalisée), le plus petit nombre est 2-126 soit environ 10-38. Il n'y a pas de nombre représentable dans l'intervalle [0, 2-126[.
Arrondis
- Au plus près(par défaut) : le flottant le plus proche de la valeur exacte;
- Vers zéro : le flottant le plus proche de 0;
- Vers plus l'infini : le plus petit flottant supérieur ou égal à la valeur exacte;
- Vers moins l'infini : le plus grand flottant inférieur ou égal à la valeur exacte;
Exemple Le nombre flottant le plus proche de N10 = 1,6 est N2 = 0 01111111 10011001100110011001101
N10 = 1 + (2-1 + 2-4 + 2-5 + 2-8 + 2-9 + 2-12 + 2-13 + 2-16 + 2-17 + 2-20 + 2-21 + 2-23) x + 2127-127 = 1,60000002384185791015625

4.3 Les flottants en Python
5. Représentation des caractères

5.1 Codage ASCII
Dans les années 60, les ordinateurs utilisent des mots de 8 octets. Le code ASCII (American Standard Code for Information Interchange) normalise la représentation des caractères. Dans ce code, le bit de poids fort b7 est toujours à 0. Entre 0016 et 2016 les caractères sont dit spéciaux (espace, tabulation, fin de ligne, etc).
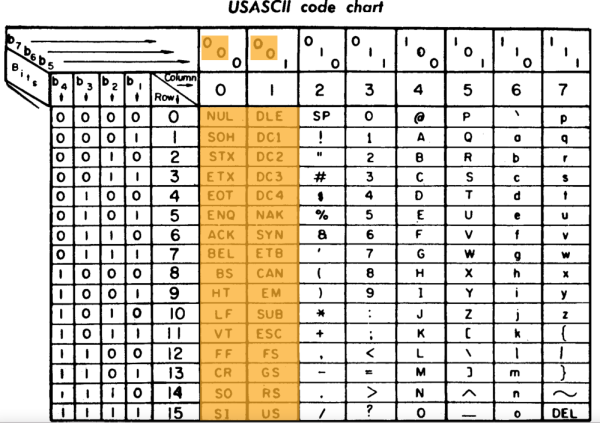
Un texte codé en ASCII est simplement une suite d'octets correspondant à la séquence de caractères.
C e c i e s t u n t e x t e ! 43 65 63 69 20 65 73 74 20 75 6e 20 74 65 78 74 65 21
Le code ASCII est encore utilisé aujourd'hui. Cependant, il a l'inconvénient de ne pas représenter les caractères accentués. Il est également limité à l'alphabet latin.
5.1 ISO 8859
- Ressource : ISO-8859-1 sur Wikipédia
A compléter

5.3 Codage Unicode
La norme Unicode, développée par un consortium du même nom, définit un jeu de caractères qui vise à inclure le plus grand nombre possible de systèmes d'écriture. Il contient à l'heure actuelle (2021) 143000 caractères couvrant 150 systèmes d'écriture ainsi que les emojis.
Cette norme définit plusieurs techniques d'encodage pour représenter les points de code de manière plus ou moins économique selon la technique choisie. Ces encodages, appelés formats de transformation universelle ou Universal Transformation Format (UTF) en anglais, portent les noms UTF-n, où n indique le nombre minimal de bits pour représenter un point de code.

5.3.1 UTF-8
Les caractères sont représentés sur 1,2,3 ou 4 octets. UTF-8 est compatible avec le code ASCII : les codes UTF-8 d'un octet avec le bit de poids fort à zéro sont les caractères du code ASCII (ainsi les programmes qui fonctionnaient sur des textes encodés en ASCII devraient continuer à fonctionner si ces mêmes textes sont encodés en UTF-8.
Les caractères codés sur plus d'un octet ont tous le bit de poids fort à 1, de telle sorte qu'ils sont en général ignorés par les logiciels qui ne connaissent que le code ASCII.
| Nb Octets | Premier “code point” | Dernier “code point” | Octet 1 | Octet 2 | Octet 3 | Octet 4 |
|---|---|---|---|---|---|---|
| 1 | U+0000 | U+007F | 0xxxxxxx | |||
| 2 | U+0080 | U+07FF | 110xxxxx | 10xxxxxx | ||
| 3 | U+0800 | U+FFFF | 1110xxxx | 10xxxxxx | 10xxxxxx | |
| 4 | U+10000 | U+10FFFF | 11110xxx | 10xxxxxx | 10xxxxxx | 10xxxxxx |
Principe de l'encodage
- Si le bit de poids fort d'un octet est à 0, alors il s'agit d'un caractère ASCII codé sur les 7 bits restants.
- Sinon, les premiers bits de poids fort de l'octet indiquent le nombre d'octets utilisés pour encoder le caractère à l'aide d'une séquence de bits à 1 et se termine par un bit à 0.
Exemple : 110xxxxx signifie que le caractère est codé sur 2 octets. - Dans le cas d'un encodage sur k octets, les k-1 octets qui suivent l'octet de poids fort doivent tous être de la forme 10xxxxxx.
Exemples
| Pt de code | point de code binaire | UTF-8 (binaire/hexa) |
|---|---|---|
| U+004B | 01001011 | 01001011 (4b) |
| U+00C5 | 11000101 | 11000011 (C3) 10000101 (85) |
| U+0A9C | 00001010 10011100 | 11100000 (E0) 10101010 (AA) 10011100 (9C) |
5.3.2 UTF16
Voir Unicode sur Wikipédia.
5.3.3 UTF-32
Voir Unicode sur Wikipédia.
5.3.4 UNICODE et Python

Exemple
- *.py
a = '\u0042' print(a) # Affichage du caractère A
A compléter

5.4 Les chaînes de caractères en Python
6. Pour aller plus loin
Résumé
- Les nombres entiers sont représentés en binaire (base 2) dans un ordinateur. La notation hexadécimale (base 16) simplifie l'écriture des nombres binaires. Il existe deux représentations des nombres stockés sur plusieurs octets, le petit et le gros boutisme, qui se différencient selon l'ordre des octets en mémoire. Le codage des nombres relatifs utilise la technique du complément à deux pour faciliter les opérations arithmétiques.
- Les nombres flottants sont une représentation approximative des nombres réels dans un ordinateur. La norme internationale IEEE 754 définit un encodage en simple (32 bits) ou double précision (64 bits) ainsi que des règles d'arrondi. Les opérations arithmétiques sur les nombres flottants n'ont pas toujours les mêmes propriétés que ces mêmes opérations sur les réels.
- Les caractères sont représentés par des entiers et des tables de correspondances sont établies par des normes (ASCII, Unicode). La norme ASCII définit un jeu restreint de 127 caractères. Le format Unicode est conçu pour représenter les caractères de toutes les langues. Il existe plusieurs formats d'encodage Unicode (UTF-8, UTF-16, UTF-32) qui se distinguent par le nombre d'octets minimum pour représenter les points de code.